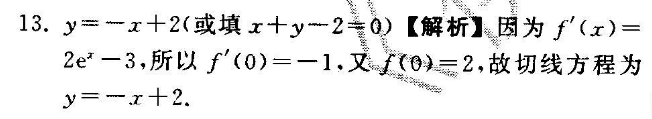2022-2023学年北京市怀柔区高二(下)期末数学试卷,以下展示关于2022-2023学年北京市怀柔区高二(下)期末数学试卷的相关内容节选,更多内容请多关注我们

1、(北京)股份有限公司 北京市怀柔区 20222023 学年度第二学期期末试卷高二数学北京市怀柔区 20222023 学年度第二学期期末试卷高二数学 2023.7 第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)若1,2x成等差数列,则(A)32x(B)3x(C)2x(D)2 x(2)函数1()f xxx在2x处的切线斜率为(A)-3 (B)34(C)54(D)5(3)已知函数()sincosf xxx,()fx为()f x的导函数,则(A)()sincosfxxx(B)()sincosfxxx(C)()sincos
2、fxxx(D)()sincosfxxx(4)一个袋中装有大小相同的 3 个白球和 2 个红球,现在不放回的取 2 次球,每次取出一个球,记“第 1 次拿出的是白球”为事件 A,“第 2 次拿出的是白球”为事件 B,则 P(B|A)=(A)14(B)310(C)35(D)12(5)已知函数()f x的导函数()fx的图象如图所示,则()f x(A)有极小值,但无极大值(B)既有极小值,也有极大值(C)有极大值,但无极小值(D)既无极小值,也无极大值(6)将一枚均匀硬币随机抛掷4次,记“正面向上出现的次数”为X,则随机变量X的期望()E X(A)1(B)2(C)3 (D)4(7)在数列na中,若1
3、1a ,*11(2,)1nnannNa,则10a(A)-1(B)1(C)12(D)2(8)若nS是等差数列na的前n项和,8(8,)nSS nnN,则(A)890,0aa(B)890,0aa(C)890,0aa(D)890,0aa(9)数列na的通项公式为()2(1,2,)nnann,若na是递增数列,则的取值范围是(A)1,)(B)2(1log,3)e(C)2(,1loge(D)(,3)(10)已知函数()3)(xf xeln x,则下面对函数 f(x)的描述正确的是(A)1()(33,)xf x (B)1()(23,)xf x(C)001()(3,),xf x (D),()()0 1min
4、f x第二部分(非选择题 共110 分)(北京)股份有限公司 二、填空题共5小题,每小题5分,共25分.(11)设函数()xxf xe,则(1)f _(12)已知随机变量X的分布列如下,且7()6E X:X01aP16p13则p _;a _(13)已知na是公比为q的等比数列,其前n项和为nS若213Sa,则q _(14)若曲线lnyxabx在0 x 处的切线方程为yx,则a _;b _(15)设随机变量的分布列如下:1 2 3 4 5 6 7 8 9 10 P 1a2a3a4a5a6a7a8a9a10a给出下列四个结论:当na为等差数列时,5615aa;当na为等差数列时,公差10d45;当
5、数列na满足12nna(n=1,2,.,9)时,10912a;当数列na满足时,211()(1,2,10)10(1)knPkk a kan n时,.其中所有正确结论的序号是_ 三、解答题共 6 小题,共 85 分.解答应写出文字说明,演算步骤或证明过程.(16)(本小题 13 分)已知等差数列的na的前 n 项和为nS,从条件、条件和条件中选择两个作为已知,并完成解答:()求na的通项公式;()若nb是等比数列,12ba,23,bS求数列nnab的前n项和nT 12nnaa;47a;24.S(17)(本小题 13 分)已知函数21()(e1)2xf xxx()求()f x的极值;()求()f
6、x在区间 1,2上的最大值和最小值(北京)股份有限公司(18)(本小题 14 分)为宣传交通安全知识,某地区中学联合开展了交通安全知识竞赛活动现从参加该活动的学生中随机抽取了 20 名学生,将他们的竞赛成绩(单位:分)用茎叶图记录如下:男 女 5 8 0 6 6 8 5 7 0 5 6 6 4 1 8 6 9 6 2 2 1 9 5 8 8()从该地区参加该活动的男生中随机抽取 1 人,估计该男生的竞赛成绩在 90 分以上的概率;()从图中 90 分以上的人中随机抽取 4 人,抽到男生的人数记为 X,求 X 的分布列和期望;()为便于普及交通安全知识,现从该地区某所中学参加知识竞赛活动的学生中随机选取 5 名男生、5名女生作为宣传志愿者,记这 5 名男生竞赛成绩的平均数为1,这 5 名女生竞赛成绩的平均数为2,能否认为12,说明理由.(19)(本小题 15 分)已知某企业生产一种产品的固定成本为 400 万元,每生产 x 万件,需另投入成本()p x万元,假设该企业年内共生产该产品x万件,并且全部销售完,每 1 件的销售收入为 100 元,且 3060()64001016150,150
4.安史之乱爆发后,朝廷失去了对东北部大部分地区的控制权,那些原忠于朝廷的藩镇也不再将大量钱粮上缴长安,朝廷只能依靠富裕的南方提供的补给勉力维持。正如杜牧所述,“今天下以江淮为国命”。这说明A.经济重心南移已经完成B.藩镇割据加重农民负担C.唐朝财政已经人不敷出D.南方经济地位不断提升
1、(北京)股份有限公司 北京市怀柔区 20222023 学年度第二学期期末试卷高二数学北京市怀柔区 20222023 学年度第二学期期末试卷高二数学 2023.7 第一部分(选择题 共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.(1)若1,2x成等差数列,则(A)32x(B)3x(C)2x(D)2 x(2)函数1()f xxx在2x处的切线斜率为(A)-3 (B)34(C)54(D)5(3)已知函数()sincosf xxx,()fx为()f x的导函数,则(A)()sincosfxxx(B)()sincosfxxx(C)()sincos
2、fxxx(D)()sincosfxxx(4)一个袋中装有大小相同的 3 个白球和 2 个红球,现在不放回的取 2 次球,每次取出一个球,记“第 1 次拿出的是白球”为事件 A,“第 2 次拿出的是白球”为事件 B,则 P(B|A)=(A)14(B)310(C)35(D)12(5)已知函数()f x的导函数()fx的图象如图所示,则()f x(A)有极小值,但无极大值(B)既有极小值,也有极大值(C)有极大值,但无极小值(D)既无极小值,也无极大值(6)将一枚均匀硬币随机抛掷4次,记“正面向上出现的次数”为X,则随机变量X的期望()E X(A)1(B)2(C)3 (D)4(7)在数列na中,若1
3、1a ,*11(2,)1nnannNa,则10a(A)-1(B)1(C)12(D)2(8)若nS是等差数列na的前n项和,8(8,)nSS nnN,则(A)890,0aa(B)890,0aa(C)890,0aa(D)890,0aa(9)数列na的通项公式为()2(1,2,)nnann,若na是递增数列,则的取值范围是(A)1,)(B)2(1log,3)e(C)2(,1loge(D)(,3)(10)已知函数()3)(xf xeln x,则下面对函数 f(x)的描述正确的是(A)1()(33,)xf x (B)1()(23,)xf x(C)001()(3,),xf x (D),()()0 1min
4、f x第二部分(非选择题 共110 分)(北京)股份有限公司 二、填空题共5小题,每小题5分,共25分.(11)设函数()xxf xe,则(1)f _(12)已知随机变量X的分布列如下,且7()6E X:X01aP16p13则p _;a _(13)已知na是公比为q的等比数列,其前n项和为nS若213Sa,则q _(14)若曲线lnyxabx在0 x 处的切线方程为yx,则a _;b _(15)设随机变量的分布列如下:1 2 3 4 5 6 7 8 9 10 P 1a2a3a4a5a6a7a8a9a10a给出下列四个结论:当na为等差数列时,5615aa;当na为等差数列时,公差10d45;当
5、数列na满足12nna(n=1,2,.,9)时,10912a;当数列na满足时,211()(1,2,10)10(1)knPkk a kan n时,.其中所有正确结论的序号是_ 三、解答题共 6 小题,共 85 分.解答应写出文字说明,演算步骤或证明过程.(16)(本小题 13 分)已知等差数列的na的前 n 项和为nS,从条件、条件和条件中选择两个作为已知,并完成解答:()求na的通项公式;()若nb是等比数列,12ba,23,bS求数列nnab的前n项和nT 12nnaa;47a;24.S(17)(本小题 13 分)已知函数21()(e1)2xf xxx()求()f x的极值;()求()f
6、x在区间 1,2上的最大值和最小值(北京)股份有限公司(18)(本小题 14 分)为宣传交通安全知识,某地区中学联合开展了交通安全知识竞赛活动现从参加该活动的学生中随机抽取了 20 名学生,将他们的竞赛成绩(单位:分)用茎叶图记录如下:男 女 5 8 0 6 6 8 5 7 0 5 6 6 4 1 8 6 9 6 2 2 1 9 5 8 8()从该地区参加该活动的男生中随机抽取 1 人,估计该男生的竞赛成绩在 90 分以上的概率;()从图中 90 分以上的人中随机抽取 4 人,抽到男生的人数记为 X,求 X 的分布列和期望;()为便于普及交通安全知识,现从该地区某所中学参加知识竞赛活动的学生中随机选取 5 名男生、5名女生作为宣传志愿者,记这 5 名男生竞赛成绩的平均数为1,这 5 名女生竞赛成绩的平均数为2,能否认为12,说明理由.(19)(本小题 15 分)已知某企业生产一种产品的固定成本为 400 万元,每生产 x 万件,需另投入成本()p x万元,假设该企业年内共生产该产品x万件,并且全部销售完,每 1 件的销售收入为 100 元,且 3060()64001016150,150







1答案.jpg)