山西省2023-2024学年度上学期期中八年级学期调研测试试题历史

山西省2023-2024学年度上学期期中八年级学期调研测试试题历史试卷答案,我们答案汇总网收集并整理关于山西省2023-2024学年度上学期期中八年级学期调研测试试题历史试卷答案得系列试题及其答案，更多试题答案请关注本网站

山西省2023-2024学年度上学期期中八年级学期调研测试试题历史试卷答案

以下是该试卷的部分内容或者是答案亦或者啥也没有，更多试题答案请关注本网站

高三数学试卷参考答案1.C【解析】本题考查集合的交集运算，考查运算求解能力，因为A=(-∞，1]，B=(-√3，W3),所以A∩B=(-√5,1].2.A【解析】本题考查复数的四则运算，考查运算求解能力.

泽+1行8+1+11则53.C【解析】本题考查命题的真假以及命题的否定，考查逻辑推理的核心素养.当x=2时，3x+4>3,当x-3时，3.x十4<3，故p为真命题，又存在量词命题的否定为全称量词命题.故选C4.D【解析】本题考查三角恒等变换，考查运算求解能力，sm(20-受)--0s20-23n0-1=-05.D【解析】本题考查平面向量，考查运算求解能力.由a⊥b,得m十4-2m=0,则m=4,所以|b|=√42十（一2）2=2√5.6.A【解析】本题考查指数、对数的运算，考查数学建模的核心素养.依题意可知当t=0时，y=6.05,即0.05十λ=6.05，入=6，所以y=0.05十6e‘,由y=005+6e≤0.1.得e≤0：解得≥h120=3n2+n3+n54.8,至少需要放登的时间为5周

7.B【解析】本题考查函数的奇偶性，考查逻辑推理的核心素养.因为定义在R上的奇函数f(x)在（一∞，0）上单调递减，且f(1)=0,所以f(x)在(0，+∞)上也是单调递减，且f(一1)=0，f(0)=0,因为定义在R上的偶函数g(x)在（一∞，0]上单调递增，且g(1)=0,所以g(x)在[0,+∞)上是单调递减，且g(-1)=0.所以x∈(0,1)U(1,十∞)满足f(x)g(x)>0.8.D【解析】本题考查数列的单调性，考查运算求解能力当n=1时，a1=S=4+λ，当n≥2时，am=Sn-Sm1=2"+2n2+λ-[2-1+2(n-1)2+入]=2-1+4n-2,则可知当n≥2时，{am}单调递增，故{an}为递增数列只需满足a2>a1,即8>4十入，解得λ<4，则实数入的取值范围是（一∞，4）.9.AC【解析】本题考查充分必要条件，考查逻辑推理的核心素养

由ab+b-a-1=0,可得(a+1)(b-1)=0,解得a=-1或b=1,故选AC10.ACD将等差数列a1,a2,a5,a1o,…记为{b},则公差d=a10)=3,a1=a2-3=1,b=3k-2,A正确.第1行的项数，第2行的项数，，第k行的项数构成以1为首项，2为公差的等差数列，即第k行共有2k一1项，则前k行共有1+26-D=项，1936=44<2021<45=2025，则a%为第45行从左边数的第852项，即位于第85列.B错误.A1=a1-3n+1a-众X(号产1-号≤3初23+1-a241C正确a=hX(宁)兴，D正确

11.BCD【解析】本题考查三角函数的图象，考查逻辑推理的核心素养.因为f）=2as(om-哥）1=6as2ar一字).所以e的最小正周期为亮-对于A,因为1f()-f()川=2，一2m=元，所以f(x)的最小正周期T=2π，所以T=2x,得w=2Ct)故A错误对于B,图象变换后得到函数)=c0s(2x十2否)，若其图象关于原点对称，则否=受十x,k∈【高三数学·参考答案第1页（共5页）】·23-95C·

8.有学者说,日耳曼法在很多方面还是比较粗糙和简单的,但日耳曼法中的一些颇具特色的法律制度和法律思想正涌动在现代的法制文明中。对此的正确理解应是,日耳曼法A.是日耳曼人部落习惯法的汇编B.奠定了近代西欧法律的基础C.所维护的政治制度影响深远D.为世界法制文明做出了贡献

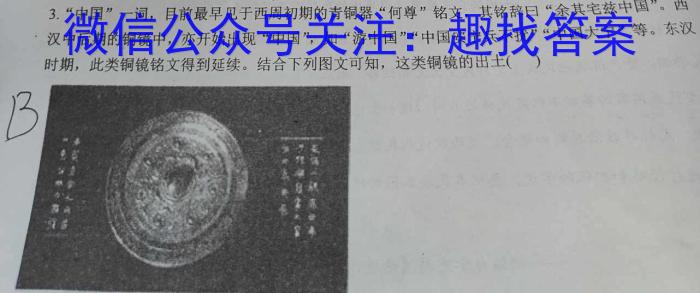
3.“中国”一词,目前最早见于西周初期的青铜器“何尊”铭文,其铭辞曰“余其宅兹中国”。西汉中后期的铜镜中,亦开始出现“中国”,如“游中国”“中国安宁兵不扰”“中国大宁”等。东汉时期,此类铜镜铭文得到延续。结合下列图文可知,这类铜镜的出土()